# 什么是数据结构?
数据结构其实没有一个官方的定义,但是民间有一些比较常见的一些定义,挑选其中三个给大家做个参考。
- 民间定义:
- “数据结构是数据对象,以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出” --- 《数据结构、算法与应用》
- “数据结构是ADT(抽象数据类型)的物理实现。” --- 《数据结构与算法分析》
- “数据结构是计算机中存储、组织数据的方式。通常情况下,精心选择的数据结构可以带来最优效率的算法。” --- 中文维基百科
- 通俗理解:
- “数据结构”就是在计算机中,存储和组织数据的方式。
# 什么是算法(Algorithm)?
- 算法的定义
- 一个有限的指令集,每条指令的描述不依赖于语言。
- 接受一些输入(有些情况下不需要输入)。
- 产生输出。
- 一定在有限步骤之后终止。
- 通俗理解
- Algorithm这个单词本意就是解决问题的办法和步骤逻辑。
- 数据结构的实现离不开算法。
# 数据结构及特性
# 线性结构 重要须知
- 数组(Array)
- 说明:
- 几乎所有的编程语言原生都支持数组类型,因此数组是最简单的内存数据结构。
- 数组通常情况下用于存储一系列同一种数据类型的值。
- 但在JavaScript里,可以在数组中保存不同类型的值。但我们还是要遵守最佳实践,别这么做(大多数语言都没这个能力)。
- 补充:普通语言的数组封装
- 常见语言的数组不能存放不同类型的数据,因此在封装时通常存放在数组中的是Object类型。
- 常见语言的数组容量不会自动改变。(需要进行扩容)。
- 常见语言的数组进行中间插入和删除操作性能比较低。
- 图示:
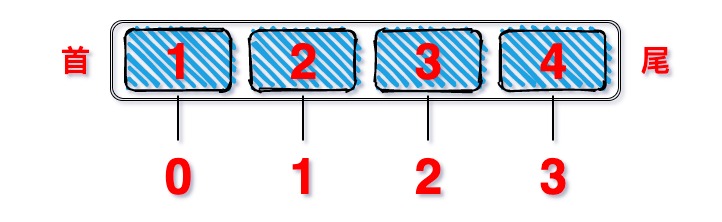
- 说明:
- 队列(Queue)
- 说明:
- 队列也是一种非常常见的数据结构,并且在程序中的应用非常广泛
- 队列是比较常见的受限的线性结构(表)。
- 普通队列
- 队列的特点:
- 遵循先进先出(FIFO<first in first out>)的原则。
- 受限之处在于它只允许在表的前端进行删除操作。
- 而在表的后端进行插入操作。
- 实现:
点击查看代码
function Queue() { this.items = []; // 将元素添加到队列 Queue.prototype.enqueue = function (value) { this.items.push(value); } // 删除队列的前端元素 Queue.prototype.dequeue = function () { return this.items.shift(); } // 查看队列的前端元素 Queue.prototype.front = function () { return this.items[0]; } // 队列是否为空 Queue.prototype.isEmpty = function () { return !this.items ? true : false; } // 队列的长度 Queue.prototype.size = function () { return this.items.length; } // 队列toString方法 Queue.prototype.toString = function () { let str = ''; for(let i = 0; i < this.items.length; i++){ str += `${this.items[i]} ` } return str.slice(0, str.length - 1);; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 - 队列的特点:
- 优先队列
- 优先队列的特点:
- 优先队列,在插入一个元素的时候会考虑该数据的优先级。
- 和其他优先级进行比较。
- 比较完成后,可以得出这个元素在队列中的正确位置。
- 其他处理方式,和普通队列的处理方式一样。
- 实现:
点击查看代码
function PriorityQueue() { // 内部类 function QueueElement(element, priority){ this.element = element; this.priority = priority; } this.items = []; // 将元素添加到队列 PriorityQueue.prototype.enqueue = function (element, priority) { // 创建QueueElement对象 let queueElement = new QueueElement(element, priority); // 判断队列是否为空 if (this.items.length === 0) { this.items.push(queueElement) } else { let added = false; for (let i = 0; i < this.items.length; i++) { if (queueElement.priority < this.items[i].priority) { this.items.splice(i, 0, queueElement); added = true; break; } } if (!added) { this.items.push(queueElement) } } } // 删除队列的前端元素 PriorityQueue.prototype.dequeue = function () { return this.items.shift(); } // 查看队列的前端元素 PriorityQueue.prototype.front = function () { return this.items[0]; } // 队列是否为空 PriorityQueue.prototype.isEmpty = function () { return !this.items ? true : false; } // 队列的长度 PriorityQueue.prototype.size = function () { return this.items.length; } // 队列toString方法 PriorityQueue.prototype.toString = function () { let str = ''; for (let i = 0; i < this.items.length; i++) { str += `${this.items[i].element}-${this.items[i].priority} ` } return str.slice(0, str.length - 1);; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 - 优先队列的特点:
- 图示:
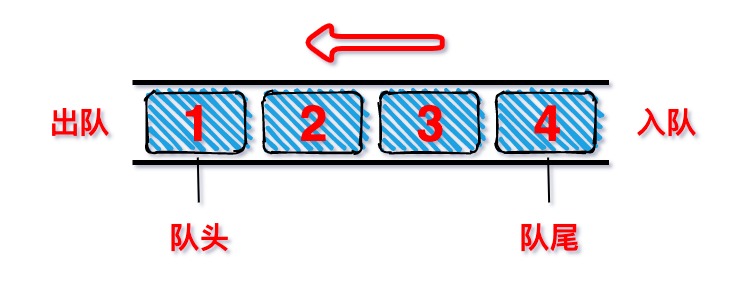
- 说明:
- 栈(Stack)
- 说明:
- 栈也是一种非常常见的数据结构,并且在程序中的应用非常广泛
- 栈是比较常见的受限的线性结构(表)。
- 栈的特点:
- 遵循先进后出(也可称后进先出)(LIFO<last in first out>)的原则。
- 只能在表一端对数据进行操作,这一端被成为栈顶,相对的,把另一端称为栈底。
- 向一个栈插入新元素,又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素。
- 从一个栈删除元素又称作出栈或退栈,
- 实现:
点击查看代码
function Stack() { this.items = []; // 将元素压入栈中 Stack.prototype.push = function (value) { this.items.push(value); } // 从栈中取出元素 Stack.prototype.pop = function () { return this.items.pop(); } // 查看栈顶元素 Stack.prototype.peek = function () { return this.items[this.items.length -1]; } // 栈是否为空 Stack.prototype.isEmpty = function () { return !this.items ? true : false; } // 获取栈中的元素个数 Stack.prototype.size = function () { return this.items.length; } // 栈toString方法 Stack.prototype.toString = function () { let str = ''; for(let i = 0; i < this.items.length; i++){ str += `${this.items[i]} ` } return str.slice(0, str.length - 1);; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37- 图示:
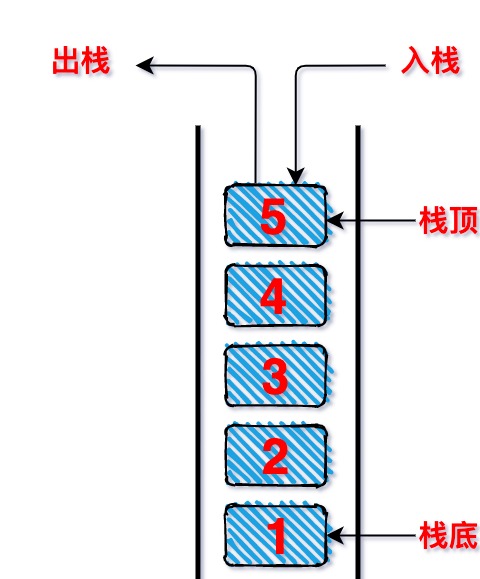
- 说明:
- 链表(LinkedList)
- 说明:
- 链表和数组一样,可以用于存储一系列的元素,但是链表和数组的实现机制完全不同。
- 链表的特点:
- 不同于数组,链表中的元素在内存中不必是连续的空间。
- 单向链表 的每个元素由一个存储 元素本身的节点 和一个 指向下一节点元素的引用(也可称指针或者连接) 组成。
- 双向链表 的每个元素由一个存储 元素本身的节点 和一个 指向上一节点和指向下一节点元素的引用(也可称指针或者连接) 组成。
- 链表无需在创建时就确定大小,并且大小可以无限的延伸下去。
- 链表在插入和删除数据时,时间复杂度可以达到O(1),相对于数组效率要高很多。
- 单(向)链表实现:
点击查看代码
function LinkedList() { // 节点类 function Node(data) { this.data = data; this.next = null; } // head属性 this.head = null; this.length = 0; // append方法,添加节点 LinkedList.prototype.append = function(data) { // 创建一个新的节点 let newNode = new Node(data); // 判断是否第一个节点 if(this.length === 0){ // 是第一个节点,直接把新节点赋值给head this.head = newNode; }else{ // 否则的话找到最后一个节点,并把新节点赋值给最后一个节点的next let currentNode = this.head; while(currentNode.next){ currentNode = currentNode.next; } currentNode.next = newNode; } // length加1 this.length += 1; } // toString方法,返回字符串数据 LinkedList.prototype.toString = function() { // 获取到首节点 let currentNode = this.head; let listStr = ''; // 循环获取每个节点 while(currentNode){ listStr += `${currentNode.data} `; currentNode = currentNode.next; } return listStr.slice(0, listStr.length - 1); } // insert方法,在指定位置插入节点 LinkedList.prototype.insert = function(position, data) { // 对边界进行限制 if(position < 0 || position > this.length){ return false; } // 创建新的node节点 let newNode = new Node(data); // 判断position是否等于0,是第一个 if(position === 0){ newNode.next = this.head; this.head = newNode; }else{ let index = 0; // 当前节点 let currentNode = this.head; // 上一节点 let previousNode = null; while(index++ < position){ previousNode = currentNode; currentNode = currentNode.next; } newNode.next = currentNode; previousNode.next = newNode; } // length加1 this.length += 1; } // get方法,获取对应位置的元素 LinkedList.prototype.get = function(position) { // 越界判断 if(position < 0 || position >= this.length){ return null; } // 定义一个初始坐标和头指针 let index = 0; let currentNode = this.head; while(index++ < position){ currentNode = currentNode.next; } return currentNode; } // indexOf方法,返回对应位置的索引 LinkedList.prototype.indexOf = function(element) { // 定义索引及头指针 let index = 0; let currentNode = this.head; // 开始查找 while(currentNode){ if(currentNode.data === element){ break; } index += 1; currentNode = currentNode.next; } // 返回结果 return currentNode ? index : -1; } // update方法,更新对应位置项的数据 LinkedList.prototype.update = function(position, data) { // 边界判断 if(position < 0 || position >= this.length){ return false; } // 定义索引及头指针 let index = 0; let currentNode = this.head; while(index++ < position){ currentNode = currentNode.next; } // 修改数据 currentNode.data = data; } // removeAt方法,从列表指定位置移除一项 LinkedList.prototype.removeAt = function(position) { // 边界判断 if(position < 0 || position >= this.length){ return false; } // 定义头指针 let currentNode = this.head; let previousNode = null; if(position === 0){ this.head = currentNode.next; }else{ let index = 0; while (index++ < position) { previousNode = currentNode; currentNode = currentNode.next; } previousNode.next = currentNode.next; } // length 减1 this.length -= 1; return currentNode; } // remove方法,从链表中移除一项 LinkedList.prototype.remove = function(data) { let position = this.indexOf(data); return this.removeAt(position); } // isEmpty方法,检测链表是否为空 LinkedList.prototype.isEmpty = function() { return this.length === 0; } // size方法,链表的元素个数 LinkedList.prototype.size = function() { return this.length; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178- 双向链表实现:
点击查看代码
function DoublyLinkedList() { // 节点 function Node(data) { this.prev = null; this.data = data; this.next = null; } this.head = null; this.tail = null; this.length = 0; // append方法,插入节点 DoublyLinkedList.prototype.append = function (data) { // 创建新节点 let newNode = new Node(data); if (this.length === 0) { this.head = newNode; this.tail = newNode; } else { newNode.prev = this.tail; this.tail.next = newNode; this.tail = newNode; } this.length += 1; } // toString方法,返回数据组成的字符串 DoublyLinkedList.prototype.toString = function () { // 返回字符串格式数据 return this.backwardString(); } // forwardString方法,输出反向字符串数据 DoublyLinkedList.prototype.forwardString = function () { // 定义变量 let currentNode = this.tail; let resultString = ''; while (currentNode) { resultString += `${currentNode.data} `; currentNode = currentNode.prev; } return resultString; } // backwardString方法,输出正向字符串数据 DoublyLinkedList.prototype.backwardString = function () { // 定义变量 let currentNode = this.head; let resultString = ''; while (currentNode) { resultString += `${currentNode.data} `; currentNode = currentNode.next; } return resultString } // insert方法,在指定位置插入节点 DoublyLinkedList.prototype.insert = function (position, data) { // 边界判断 if (position < 0 || position > this.length) { return false; } // 创建新的节点 let newNode = new Node(data); // 判断原来的链表是否为0 if (this.length === 0) { this.head = newNode; this.tail = newNode; } else { if (position === 0) { // 判断插入位置是否为0 this.head.prev = newNode; newNode.next = this.head; this.head = newNode; } else if (position === this.length) { // 判断插入的是不是最后一个 newNode.prev = this.tail; this.tail.next = newNode; this.tail = newNode; } else { // 其他情况插入中间 let index = 0; let currentNode = this.head; while (index++ < position) { currentNode = currentNode.next; } // 修改指针 newNode.next = currentNode; newNode.prev = currentNode.prev; currentNode.prev.next = newNode; currentNode.prev = newNode; } } // 索引 +1 this.length += 1; return true; } // get方法,获取节点数据 DoublyLinkedList.prototype.get = function (position) { // 边界判断 if (position < 0 || position >= this.length) { return null; } // 定义变量 let currentNode = this.head; let index = 0; while (index++ < position) { currentNode = currentNode.next; } // 返回节点的数据 return currentNode.data; } // indexOf方法,获取节点索引 DoublyLinkedList.prototype.indexOf = function (data) { // 定义变量 let currentNode = this.head; let index = 0; while (currentNode) { if (currentNode.data === data) { // 返回索引 return index; } index += 1; currentNode = currentNode.next; } // 找不到返回负数 return -1; } // update方法,修改指定位置的数据 DoublyLinkedList.prototype.update = function (position, data) { // 边界判断 if (position < 0 || position >= this.length) { return false; } // 定义变量 let currentNode = this.head; let index = 0; // 查找节点 while (index++ < position) { currentNode = currentNode.next; } // 修改数据 currentNode.data = data; return true; } // removeAt方法,移除指定位置元素 DoublyLinkedList.prototype.removeAt = function (position) { // 边界判断 if (position < 0 || position >= this.length) { return null; } let currentNode = this.head; // 判断情况 if (this.length === 1) { // 是否只有一个节点 this.head = null; this.tail = null; } else { if (position === 0) { // 判断删除的是否是第一个节点 this.head.next.prev = null; this.head = this.head.next; } else if (position === this.length - 1) { // 判断是否最后一个节点 this.tail.prev.next = null; this.tail = this.tail.prev; } else { // 其他中间情况 let index = 0; while (index++ < position) { currentNode = currentNode.next; } currentNode.prev.next = currentNode.next; currentNode.next.prev = currentNode.prev; } } this.length -= 1; return currentNode.data; } // remove方法 DoublyLinkedList.prototype.remove = function (data) { // 根据data获取下标 let index = this.indexOf(data); // 根据index删除对应位置的元素 return this.removeAt(index); } // isEmpty方法,判断链表是否为空 DoublyLinkedList.prototype.isEmpty = function () { return this.length === 0; } // size方法,查看链表节点个数 DoublyLinkedList.prototype.size = function () { return this.length; } // getHead查看头节点数据 DoublyLinkedList.prototype.getHead = function () { return this.head.data; } // getTail方法,查看尾节点数据 DoublyLinkedList.prototype.getTail = function () { return this.tail.data; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226- 图示

- 说明:
- 哈希表
- 说明:
- 哈希表通常是基于数组进行实现的,但是相对于数组,它也有很多优势。
- 它的结构就是数组,但是神奇的地方在于对下标值的一种变换,这种变换我们可以称之为哈希函数,通过哈希函数可以获取到HashCode。
- 优缺点:
- 特点:
- 它可以提供非常快速的插入、删除、查找操作。
- 无论多少数据,插入和删除值需要接近常量的时间:即O(1)的时间级。
- 哈希表的速度比树还要快,基本可以瞬间查找到想要的元素。
- 哈希表相对于树来说编码要容易的多。
- 不足:
- 哈希表中的数据是没有顺序的,所以不能以一种固定的方式(如从小到大)来遍历其中的元素。
- 通常情况下,哈希表中的key是不允许重复的,不能放置相同的key,用于保存不同的元素。
- 特点:
- 哈希化:
- 哈希化: 将 大数字 转化成 数组范围内下标 的过程,我们就称之为哈希化。
- 哈希函数: 通常我们会将 单词 转成 大数字,大数字 在进行 哈希化 的代码实现放在一个函数中,这个函数我们称为哈希函数。
- 哈希表:最终将数据插入到的这个数组,对整个结构的封装,我们就称之为是一个哈希表。
- 冲突解决:(常见的有以下两种方法)
说明:虽然通过哈希化对数字进行了处理,但是依然还会有少部分重复的情况,这种情况我们称为冲突。- 链地址法(也称为:拉链法)。
- 简单理解就是,如果通过哈希化后得到地址,发现已经有一个元素了,就把原来的元素和新元素一起封装成一个数组或者链表,再存到原来的位置。
- 开放地址法。
- 开放地址法的主要工作方式是寻找空白的单元格来添加重复的数据。(寻找空白单元格有三种方法:分别是线性探测 、 二次探测 、 再哈希)。
- 线性探测:就是线性查找空白的单元格。
- 插入:从index位置每次+1一直往后查找,直到找到合适的位置(即空白的单元格)插入。
- 查找:通过index取到相应位置的值,再比对与查找的是否相等,不是则依次往后查并且往后查遇到空位置就停止(特殊情况:删除元素的时候应把相应位置设为 -1 否则会影响后续查找)。
- 存在问题:比如刚开始没有数据的时候经过哈希化得到2-3-4-5-6连续的下标,那我下一次查找的时候就要一直连续的查找,直到查找到有效位置。 这种一连串的单元 就称为 聚集,会存在一定的性能问题。
- 二次探测:主要是优化了探测时的步长。
- 线性探测可以堪称是步长为1,如从下标x开始,那么线性探测应该就是x+1,x+2,x+3,每次走1步。
- 二次探测在此基础上进行了优化:如从下标值x开始,x+12,x+22,x+32,这样就可以一次探测很长一段距离。
- 存在问题:当他们依次累加的时候步长依然是相同的,也就会这种情况下会造成步长不一样的聚集,还是会影响效率(当然这一种会比前一种的可能性要小一些)。
- 再哈希:把关键字用另外一个哈希函数,再做一次哈希化, 用这次的哈希化的结果作为步长,对于指定的关键字, 步长,在整个探测中是不变的,不过 不同的关键字 使用 不同的步长。
- 特点:
- 和第一个哈希函数不同(不要再使用上一次的哈希函数,不然结果还是同样的位置)。
- 不能输出为0(否则,将没有步长,每次探测都是原地踏步,算法就进入了死循环)。
- 解决办法:
- 专家给出的比较好了一个哈希函数,就是:stepSize(步长) = constant(质数) - (key(关键字) % constant(质数))。
- 其中 constant是质数, 且小于数组的容量,之所以要模质数是因为对于特殊数据合数会发生大量碰撞,而质数可以避免这种情况,能让数据在哈希表内更均匀的分布。
- 例如:stepSize = 5 - (key % 5),满足要求,并且结果不可能为0。
- 特点:
- 链地址法(也称为:拉链法)。
- 效率优化:
- 因为此实例是采用的链地址法, loadFactor(装载因子) 可以大于1,所以这个哈希表可以无限制的插入新数据。
- 随着数据量的增多,每一个index对应的bucket会越来越长,所以就会造成效率的降低。
- 所以应该在适当的时候对数组进行扩容,比如扩容的两倍。
- 一般在loadFactor(装载因子) > 0.75的情况下,就需要进行扩容。
- 当然有扩容 肯定就会有 缩容,有些时候可能一直对数组内的数据进行删除,假设原先用一个1000的数组存储600个元素,其实还算合理的,然后可能一直删,最后只剩下12个元素了,那用1000空间来存12个元素是不是有点浪费空间,这时候就应该进行缩容。
- 实现:
点击查看代码
// 封装hash表(基于链地址法实现) function hashTable() { // 属性 // 存放元素 this.storage = []; // 表示数组已经存放的元素个数 this.count = 0; // 记录数组的长度 this.limit = 7; // 方法 // hash函数 hashTable.prototype.hashFunc = function (str, size) { // 1. 定义hashCode变量 let hashCode = 0; // 2. 霍纳算法,来计算hashCode的值 for (let i = 0; i < str.length; i++) { hashCode = 37 * hashCode + str.charCodeAt(i); } // 取余操作 let index = hashCode % size; return index; } // 新增及修改 hashTable.prototype.put = function (key, value) { // 1.根据key获取index let index = this.hashFunc(key, this.limit); // 2.根据key取出对应的bucket let bucket = this.storage[index]; // 3.判断该bucket是否为null if (bucket == null) { bucket = []; this.storage[index] = bucket } // 4.判断是否是修改数据 for (let i = 0; i < bucket.length; i++) { let tuple = bucket[i]; if (tuple[0] === key) { tuple[1] = value; return; } } // 5.进行添加操作 bucket.push([key, value]); // 6.总元素加1 this.count += 1; // 判断是否需要扩容,如果元素总数大于容器总长度的0.75就扩容 if (this.count > this.limit * 0.75) { let newSize = this.limit * 2; let newPrime = this.getPrime(newSize); this.resize(newPrime); } } // 获取相关项值 hashTable.prototype.get = function (key) { // 1.获取index let index = this.hashFunc(key, this.limit); // 2.获取buket let bucket = this.storage[index]; // 3.如果buket等于null直接返回 if (bucket == null) { return null; } // 4.如果有buket,则进行线性查找 for (let i = 0; i < bucket.length; i++) { let tuple = bucket[i]; if (tuple[0] === key) { return tuple[1]; } } // 5.依然没有找到返回null return null; } // 删除相关项 hashTable.prototype.remove = function (key) { // 通过key获取index值 let index = this.hashFunc(key, this.limit); // 通过index获取bucket let bucket = this.storage[index]; // 如果为不存在则返回null if (bucket == null) { return null; } // 如果有值,则进行线性查找,如果找到则删除,没有找到则返回null for (let i = 0; i < bucket.length; i++) { let tuple = bucket[i] if (tuple[0] === key) { bucket.splice(i, 1); this.count -= 1; // 缩小容量,判断当前的元素总数小于容器总长度的0.25的时候就缩小 if (this.limit > 7 && this.count < this.limit * 0.25) { let newSize = this.limit / 2 let newPrime = this.getPrime(newSize); this.resize(Math.floor(newPrime)); } return tuple[1]; } } return null; } // hash表是否为空 hashTable.prototype.isEmpty = function () { // hash表是否为空 return this.count === 0; } // hash表元素个数 hashTable.prototype.size = function () { // hash表是否为空 return this.count; } // hash表扩容/缩容 hashTable.prototype.resize = function (newLimit) { // 1.保存旧的数组数据 let oldStorage = this.storage; // 2.重置所有数据 this.storage = []; this.count = 0; this.limit = newLimit; // 3.遍历oldStorage所有的bucket for (let i = 0; i < oldStorage.length; i++) { // 3.1取出对应的bucket let bucket = oldStorage[i]; // 3.2判断bucket是否为null if (bucket == null) { continue; } // 3.3如果不为空,那么取出数据重新插入 for (let j = 0; j < bucket.length; j++) { let tuple = bucket[j]; this.put(tuple[0], tuple[1]); } } } // 判断是否是质数 hashTable.prototype.isPrime = function (num) { // 求num的平方根 let temp = parseInt(Math.sqrt(num)); // 循环判断 for (let i = 2; i <= temp; i++) { if (num % i === 0) { return false } } return true; } hashTable.prototype.getPrime = function (num) { while (!this.isPrime(num)) { num++ } return num } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185 - 说明:
# 非线性结构 重要须知
- 树
- 特点:
- 树(tree)n(n>=0)个节点构成的有限集合。
- 当n = 0时,称为空树。
- 对于任何一颗非空树(n>0),它具备以下性质:
- 树中有一个称为 根(root) 的特殊节点,用r表示。
- 其余节点可分为m(m>0)个互不相交的有限集T1,T2,Tm,其中每个集合本身又是一颗树,称为原来树的 “子树(subTree)” 。
- 二叉树的遍历常见的三种方式:
- 先(前)序遍历:
- 先访问根节点。
- 后遍历其左子树。
- 再遍历其右子树。
- 图示:
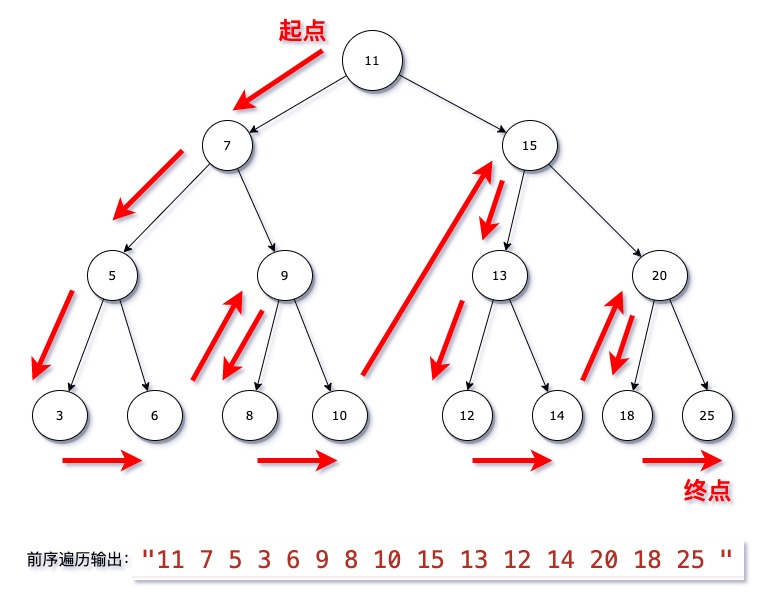
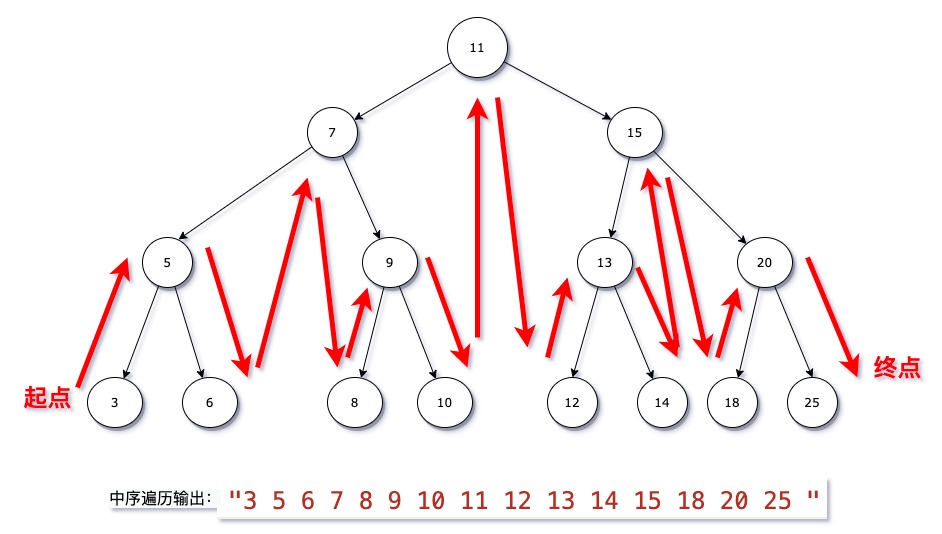
- 中序遍历:
- 先遍历其左子树。
- 后访问根节点。
- 再遍历其右子树。
- 图示:
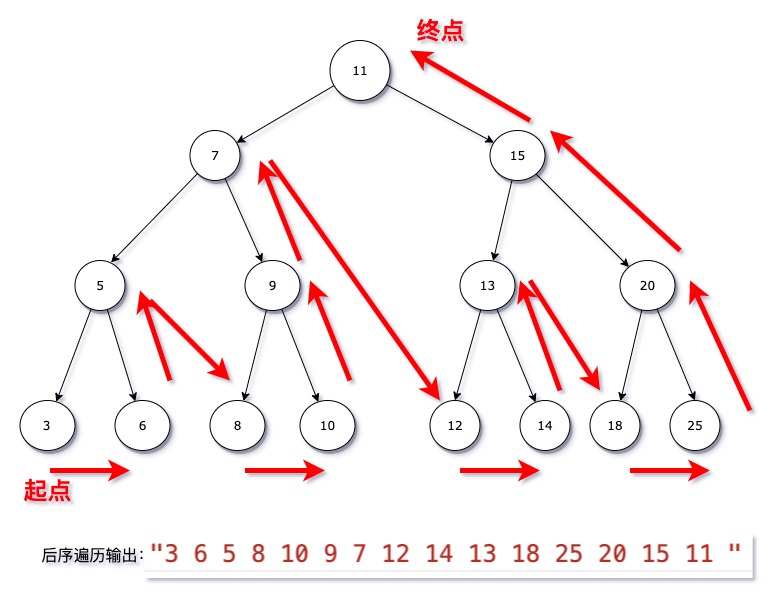
- 后续遍历:
- 先遍历其左子树。
- 后遍历其右子树。
- 访问根节点。
- 图示:
- 先(前)序遍历:
- 二叉树:
- 特点:
- 如果树中每个节点最多只能有两个子节点,这样的树就称为二叉树。
- 二叉树可以为空,也就是没有节点。
- 若不为空,则它是由根节点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。
- 特点:
- 完美二叉树:
- 特点:
- 完美二叉树,也称为满二叉树。
- 在二叉树中,除了最下一层的叶节点外,每层节点都有2个子节点,就构成了满二叉树。
- 特点:
- 完全二叉树:
- 特点:
- 除二叉树的最后一层外,其他各层的节点数都达到最大个数。
- 且最后一层从左向右的叶子节点连续存在,只缺右侧若干节点。
- 完美二叉树是特殊的完全二叉树。
- 特点:
- 二叉搜索树:
- 特点:
- 二叉搜索树(BST),也称 二叉排序树或二叉查找树。
- 二叉搜索树是一颗二叉树,可以为空。
- 如果不为空,需要满足以下性质:
- 非空左子树的所有键值小于其根节点的键值。
- 非空右子树的所有键值大于其根节点的键值。
- 左、右子树本身也都是二叉搜索树。
- 相对 较小的值 总是保存在 左节点 上,相对 较大的值 总是保存在 右节点 上。
- 实现:
点击查看代码
// 封装二叉搜索树 function BinarySearchTree() { // 创建节点 function Node(key) { this.key = key; this.left = null; this.right = null; } // 属性 this.root = null; // insert插入方法 BinarySearchTree.prototype.insert = function (key) { // 创建根节点 let newNode = new Node(key); // 判断根节点是否有值 if (this.root === null) { this.root = newNode; } else { this.insertNode(this.root, newNode); } } BinarySearchTree.prototype.insertNode = function (node, newNode) { if (newNode.key < node.key) { // 向左查找 if (node.left === null) { node.left = newNode; } else { this.insertNode(node.left, newNode); } } else { // 向右查找 if (node.right === null) { node.right = newNode; } else { this.insertNode(node.right, newNode); } } } // 搜搜特定的值 BinarySearchTree.prototype.search = function (key) { // 获取根节点 let node = this.root; // 查找特定key while (node !== null) { if (key < node.key) { node = node.left; } else if (key > node.key) { node = node.right; } else { return true; } } return false; } // 先序遍历 BinarySearchTree.prototype.preOrderTraverse = function (handler) { this.preOrderTraverseNode(this.root, handler); } BinarySearchTree.prototype.preOrderTraverseNode = function (node, handler) { if (node !== null) { // 处理经过的节点 handler(node.key); // 处理经过的左子节点 this.preOrderTraverseNode(node.left, handler); // 处理经过的右子节点 this.preOrderTraverseNode(node.right, handler); } } // 中序遍历 BinarySearchTree.prototype.middleOrderTraverse = function (handler) { this.middleOrderTraverseNode(this.root, handler); } BinarySearchTree.prototype.middleOrderTraverseNode = function (node, handler) { if (node !== null) { // 处理经过的左子节点 this.middleOrderTraverseNode(node.left, handler); // 处理经过的节点 handler(node.key); // 处理经过的右子节点 this.middleOrderTraverseNode(node.right, handler); } } // 后序遍历 BinarySearchTree.prototype.postOrderTraverse = function (handler) { this.postOrderTraverseNode(this.root, handler); } BinarySearchTree.prototype.postOrderTraverseNode = function (node, handler) { if (node !== null) { // 处理经过的左子节点 this.postOrderTraverseNode(node.left, handler); // 处理经过的右子节点 this.postOrderTraverseNode(node.right, handler); // 处理经过的节点 handler(node.key); } } // 获取最小值 BinarySearchTree.prototype.min = function () { // 获取根节点 let node = this.root; let key = null; // 依次向左查找,直到节点的为null while (node !== null) { key = node.key; node = node.left; } return key; } // 获取最大值 BinarySearchTree.prototype.max = function () { // 获取根节点 let node = this.root; let key = null; // 依次向右查找,直到为null while (node !== null) { key = node.key; node = node.right; } return key; } // 删除某项 BinarySearchTree.prototype.remove = function (key) { // 定义临时保存的变量 let current = this.root; let parent = null; let isLeftChild = true; // 寻找要删除的节点 while (current.key !== key) { parent = current; if (key < current.key) { isLeftChild = true; current = current.left; } else { isLeftChild = false; current = current.right; } // 如果发现current已经指向null,那么说明没有找到要删除的数据 if (current === null) { return false; } } // 删除的节点是叶子节点 if (current.left === null && current.right === null) { if (current == this.root) { this.root == null } else if (isLeftChild) { parent.left = null } else { parent.right = null } } else if (current.right === null) { // 4.删除有一个子节点的节点 if (current == this.root) { this.root = current.left } else if (isLeftChild) { parent.left = current.left } else { parent.right = current.left } } else if (current.left === null) { if (current == this.root) { this.root = current.right } else if (isLeftChild) { parent.left = current.right } else { parent.right = current.right } } else { // 1.获取后继节点 var successor = this.getSuccessor(current) // 2.判断是否是根节点 if (current == this.root) { this.root = successor } else if (isLeftChild) { parent.left = successor } else { parent.right = successor } // 3.将删除节点的左子树赋值给successor successor.left = current.left } } // 找后继的方法 BinarySearchTree.prototype.getSuccessor = function (delNode) { // 1.使用变量保存临时的节点 var successorParent = delNode var successor = delNode var current = delNode.right // 要从右子树开始找 // 2.寻找节点 while (current !== null) { successorParent = successor successor = current current = current.left } // 3.判断寻找的后继节点是否直接就是delNode的right节点 if (successor !== delNode.right) { successorParent.left = successor.right successor.right = delNode.right } return successor } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236 - 特点:
- 红黑树:
- 特点:
- 必须符合二叉搜索树的基本规则。
- 节点是红色和黑色。
- 根节点是黑色。
- 每个叶子节点都是黑色的空节点(NLA节点)。
- 每个红色节点的两个子节点都是黑色。(从每个叶子节点到根节点的所有路径上不能有两个连续的红色节点)。
- 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。
- 红黑树的平衡:
- 插入一个新节点时,有可能树不再平衡,可以通过三种方式的变换,让树保持平衡分别是:换色、左旋转、右旋转。
- 变色:为了重新符合红黑树的规则,尝试把 红色节点变为黑色,或者把 黑色节点变成红色。
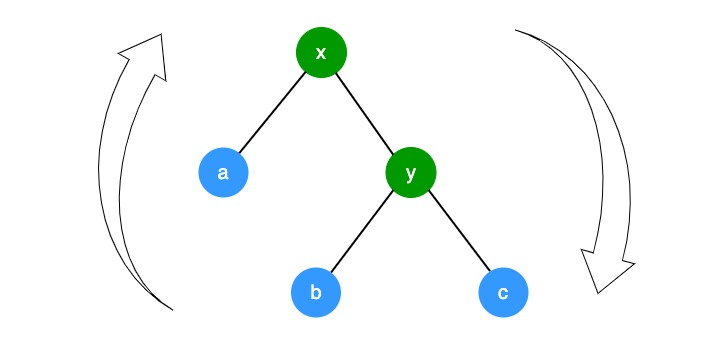
- 左旋转:逆时钟旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
- 右旋转:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
- 红黑树变换旋转图示:
- 特点:
- 特点:
- 图
- 特点:
- 图结构是一种与树结构有些相似的数据结构。
- 图论是数学的一个分支,并且,在数学的概念上,树是图的一种 。
- 有一组顶点:通常用V(vertex)表示顶点的集合。
- 有一组边:通常用E(edge)表示边的集合。
- 边是顶点和顶点之间的连线。
- 是用一个二维数组来表示图的。
- 生活中的案例:
- 比如常见的地铁线路图。
- 实现:
点击查看代码
function Graph() { // 属性 顶点(数组)/边(字典) this.vertexes = []; // 顶点 this.edges = new Dictionary(); // Dictionary是之前封装好了的字典方法 // 方法 // 添加顶点的方法 Graph.prototype.addVertexes = function(v) { this.vertexes.push(v); this.edges.set(v, []); } // 添加边的方法 Graph.prototype.addEdges = function(v1, v2) { this.edges.get(v1).push(v2); this.edges.get(v2).push(v1); } // 实现tostring方法 Graph.prototype.toString = function() { let resultStr = ''; // 遍历所有的顶点,以及顶点对应的边 for(let i = 0; i < this.vertexes.length; i++) { resultStr += this.vertexes[i] + '->'; let vEdges = this.edges.get(this.vertexes[i]); for(let j = 0; j < vEdges.length; j++) { resultStr += vEdges[j] + ' '; } resultStr += '\n'; // 为了方便打印查看 } return resultStr; } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36- 图的遍历:
- 深度优先遍历(DFS):基于队列,入队列的顶点先被探索。
- 广度优先遍历(BFS):基于栈或者使用递归,通过将顶点存入栈中,顶点是沿着路径被探索的,存在新的相邻顶点就去访问。
- 特点:
# 其他 重要须知
- 集合
- 说明:
- 集合通常是由一组无序的、不能重复的元素构成。
- 特点:
- 可以看成是特殊的数组。
- 特殊之处在于里面的元素没有顺序、且不能重复。
- 没有顺序意味着不能通过下标值进行访问,不能重复意味着相同的对象在集合中只会存在一份。
- 集合实现:
点击查看代码
function Set(){ // 属性 this.items = {}; // 方法 // add方法,添加项 Set.prototype.add = function(value){ // 判断集合中是否已包含了该元素 if(this.has(value)){ return false; } // 将元素添加到集合中 this.items[value] = value; // 操作成功返回true return true; } // remove方法,移除某项 Set.prototype.remove = function (value) { // 判断集合中是否有该元素 if(!this.has(value)){ return false; } // 删除元素 delete this.items[value]; return true; } // has方法,查找有无该项 Set.prototype.has = function (value) { return this.items.hasOwnProperty(value); } // clear方法,清空集合 Set.prototype.clear = function () { this.items = {}; } // size方法,获取集合长度 Set.prototype.size = function () { return Object.keys(this.items).length; } // values方法,获取该集合的key Set.prototype.values = function () { return Object.keys(this.items); } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 - 并集
- 并集说明:
- 如集合 A 是集合 B 的并集,其含义是:x(元素)存在于 A 中,或x(元素)也存在于 B 中。
- 实现:
点击查看代码
// 并集 Set.prototype.union = function (otherSet) { // 创建一个新的集合 let unionSet = new Set(); // 将setA集合的元素添加到新集合中 let values = this.values(); for (let i = 0; i < values.length; i++) { unionSet.add(values[i]); } values = otherSet.values(); // 判断setB中的元素,需不需要加入到新集合中 for (let i = 0; i < values.length; i++) { unionSet.add(values[i]); } return unionSet; }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- 并集说明:
- 交集
- 交集说明:
- 如集合 A 是集合 B 的交集,其含义是:x(元素)存在于 A 中,且x(元素)也存在于 B 中。
- 实现:
点击查看代码
// 交集 Set.prototype.intersection = function (otherSet) { // 创建一个新的集合 let intersectionSet = new Set(); // 从A中取出一个元素,判断是否同时存在于B中,存在则放入新集合中 let values = this.values(); for (let i = 0; i < values.length; i++) { let item = values[i]; if (otherSet.has(item)) { intersectionSet.add(item); } } return intersectionSet }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- 交集说明:
- 差集
- 差集说明:
- 如集合 A 是集合 B 的差集,其含义是:x(元素)存在于 A 中,且x(元素)不存在于 B 中。
- 实现:
点击查看代码
// 差集 Set.prototype.difference = function (otherSet) { // 定义一个新的集合 let differenceSet = new Set(); // this-集合A,otherSet-集合B let values = this.values(); // 遍历集合A,如果发现集合A中的元素不在集合B中,不在集合B中就添加到新集合 for (let i = 0; i < values.length; i++) { let item = values[i] if (!otherSet.has(item)) { differenceSet.add(item) } } return differenceSet; }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 - 差集说明:
- 子集
- 子集说明:
- 如集合 A 是集合 B 的子集,其含义是:集合 A 中的每一个元素也需要存在于集合 B 中。
- 实现:
点击查看代码
// 子集 Set.prototype.subset = function (otherSet) { // this-集合A,otherSet-集合B let values = this.values(); // 遍历集合A,如果发现集合A中的元素不在集合B中,就返回false否则返回true for (let i = 0; i < values.length; i++) { let item = values[i]; if (!otherSet.has(item)) { return false; } } return true; }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 - 子集说明:
- 说明:
- 字典
- 说明:
- 字典通常是由多个键值对组成的元素构成。
- 特点
- 字典的主要特点是一一对应的关系。
- 字典中的key是不可以重复的,但value可以重复,并且字典中的key是无序的。
- 实现:
点击查看代码
function Dictionary() { // 字典属性 this.item = {} // 操作方法 Dictionary.prototype.set = function (key, value){ // 添加 this.item[key] = value; } Dictionary.prototype.remove = function (key) { // 移除某项 if(!this.has(key)){ return false; } delete this.item[key] return true; } Dictionary.prototype.has = function (key) { // 查找是否有此项 return this.item.hasOwnProperty(key); } Dictionary.prototype.get = function (key) { // 获取此项的值 return this.has(key) ? this.item[key] : undefined; } Dictionary.prototype.clear = function () { // 清空字典 this.item = {}; } Dictionary.prototype.size = function () { // 获取字典元素个数 return Object.keys(this.item).length; } Dictionary.prototype.keys = function () { // 获取字典的key列表 return Object.keys(this.item); } Dictionary.prototype.values = function () { // 获取字典的值列表 return Object.values(this.item); } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50 - 说明:
# 算法相关
# 时间复杂度与空间复杂度的分析
# 算法思想
搜索(BFS,DFS,回溯,二分等)
暴力优化(双指针,单调栈,前缀和等)
动态规划
分治
贪心
# 学习路线
- 复杂度分析:如何衡量算法的性能?
- 基础的数据结构:线性数据结构 (数组,链表,栈,队列,哈希表)
- 基础的数据结构:非线性数据结构 (树 和 图)
- 排序算法:经典排序算法
- 递归: 一种”高级“的思维技巧
- 暴力搜索篇: 回溯,BFS, DFS
- 暴力优化篇:剪枝,滑动窗口,双指针,单调栈
- 高级搜索篇:二分法与位运算
- 动态规划篇:记忆化搜索与动态规划
- 分治:大事化小,小事化了
- 贪心:简单高效但”不靠谱“的算法
- 逆向思考